Writing a proof | Maths | Quizalize & Oak National Academy

Starter quiz

Which of these is equivalent to $(n+5)^2-(n+1)^2$ ?

$8n + 24$ ✓

$9n + 23$

$12n + 26$

$n^2 + 24$

$2n^2 + 12n + 26$
If $n$ is an integer, which of these must be true for the expression $12n + 60$ ?

It is aways odd.

It is always a multiple of 3. ✓

It is always a multiple of 5.

It is always a multiple of 6. ✓

It is always a multiple of 12. ✓
Which is the correct first step for the proof that "the square of any even number is a multiple of 4"?
Which of these could be a general form for any 3 consecutive integers?

$n, n+1, n+2$ where $n$ is an integer ✓

$2n, 2n+1, 2n+2$ where $n$ is an integer

$2n, 2n+2, 2n+4$ where $n$ is an integer

$n-1, n, n+1$ where $n$ is an integer ✓

$2n+1, 2n+3, 2n+5$ where $n$ is an integer
Which is the correct first step for the proof that "the product of any two multiples of 3 is a multiple of 9"?
Starting with the first step, arrange these steps so that they form a complete proof for "the sums of the squares of two odd integers is even", (assume $n$ and $m$ are integers).

1

⇔

Take two odd integers $2n + 1$ and $2m + 1$ .

2

⇔

$(2n+1)^2 + (2m + 1)^2$

3

⇔

$4n^2 + 4n + 1 + 4m^2 + 4m + 1$

4

⇔

$4n^2 + 4m^2 + 4n + 4m + 2$

5

⇔

$2(2n^2 + 2m^2 + 2n + 2m + 1)$

6

⇔

Any integer multiplied by 2 is an even number.

7

⇔

The sum of the squares of two odd integers is even.

Exit quiz

Arrange these statements into the correct order to prove: "For any three consecutive even integers, the difference between the squares of the first and the last number is 8 times the middle number".

1

⇔

There are 3 consecutive even integers $2n, 2n+2, 2n+4$ ( $n$ is an integer).

2

⇔

$(2n+4)^2-(2n)^2$

3

⇔

$4n^2+16n + 16 - 4n^2$

4

⇔

$16n + 16$

5

⇔

$8(2n + 2)$

6

⇔

The middle number was $2n +2$ so this is 8 times that.

7

⇔

Therefore we have proven the original statement.
The first step to the proof "If $n$ is an integer $(n+6)^2-(n+2)^2$ is a multiple of 8" is shown. Which is the correct next step?

$8n + 32$

$n^2 + 36 - (n^2 + 4)$

$n^2 + 6n + 36 - n^2 - 2n - 4$

$n^2 + 12n + 36 - n^2 + 4n + 4$

$n^2 + 6n + 6n + 36 - ( n^2 + 2n + 2n + 4)$ ✓
Izzy wants to prove that $(n+6)^2-(n+2)^2$ is a multiple of 8 for any integer $n$ . Which of these is equivalent to this expression?

$8(n+1)$

$8(n+4)$ ✓

$8(2n+5)$

$8(n^2+2 + 1)$
The first step to the proof that "The product of any two multiples of 3 is a multiple of 9" is shown. What is the best next step?

If something is a multiple of 3 it is also a multiple of 9

$9nm$ is a multiple of 9

$3n + 3m \equiv 3(n+m)$

Therefore the product of two multiples of 3 is a multiple of 9

$3n \times 3m \equiv 9nm$ ✓
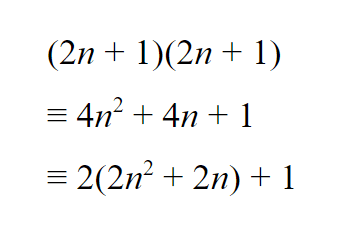Here are some steps to a proof Aisha is constructing. What do you think she is trying to prove?

Any two odd numbers have an odd product.

Any integer squared is odd.

An odd number squared is always odd. ✓

An odd number squared is one more than a multiple of 4.

The product of consecutive odd numbers cannot be a multiple of 4.
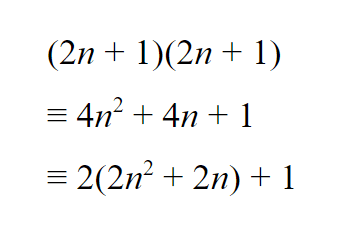Here are some steps to a proof Aisha is constructing. Why is this not a complete proof?

The generalisation has not been explained. ✓

Too many steps have been skipped in the algebraic manipulation.

There is no conclusion. ✓

The expression has not been fully factorised.

The brackets have been expanded incorrectly.

Worksheet

Loading worksheet ...

Presentation

Loading presentation ...

Video

Lesson Details

Key learning points

Any algebraic expression must be defined so that it is clear what it represents.
Algebraic expressions can be manipulated to create a different form that is equal.
This manipulation can be used to prove or show a result.

Common misconception

Pupils may think it is acceptable to use the same letter for all expressions.

It may be acceptable for the letter to be the same but that depends on what the letter is representing.

Keywords

Conjecture - A conjecture is a (mathematical) statement that is thought to be true but has not been proved yet.
Generalise - To generalise is to formulate a statement or rule that applies correctly to all relevant cases.