Multiple approaches to logical arguments | Maths | Quizalize & Oak National Academy

Starter quiz

If one shape can fit exactly on top of another using rotation, reflection or translation they are __________.

compound

congruent ✓

invariant

isosceles

regular
The interior angles of any pentagon sum to ______°.

'540' ✓
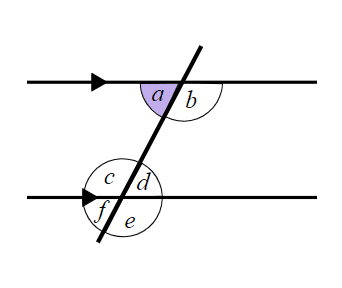The diagram shows two parallel lines and a transversal. Which angle is the alternate angle to $a$ ?

$b$

$c$

$d$ ✓

$e$

$f$
The diagram shows two parallel lines and a transversal. Which angle is the corresponding angle to $a$ ?

$b$

$c$

$d$

$e$

$f$ ✓
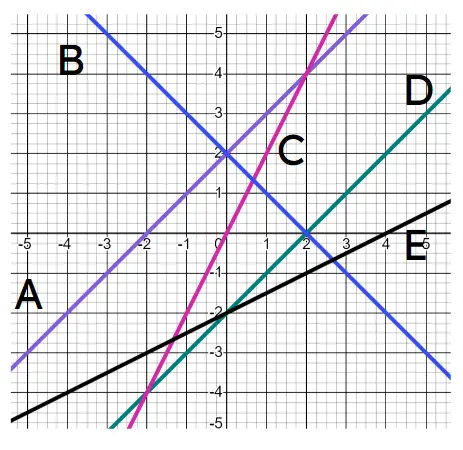Use the diagram to match the lines to their equations.

A (purple)

⇔

$y=x+2$ ✓

B (blue)

⇔

$y=-x+2$ ✓

C (pink)

⇔

$y=2x$ ✓

D (green)

⇔

$y=x-2$ ✓

E (black)

⇔

$y={1\over2}x-2$ ✓
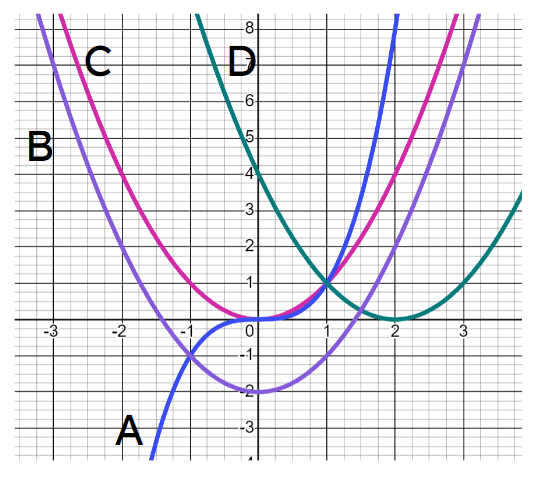Use the diagram to match the curves to their equations.

A (blue)

⇔

$y = x^3$ ✓

B (purple)

⇔

$y= x^2 - 2$ ✓

C (pink)

⇔

$y = x^2$ ✓

D (green)

⇔

$y = (x-2)^2$ ✓

Exit quiz

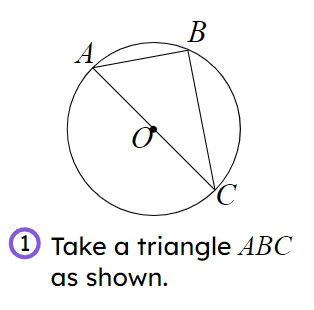What is the next step for the proof of the circle theorem "The angle in a semicircle is a right angle"?

The radius $OB$ can be drawn to split $ABC$ into 2 isosceles triangles. ✓

The angle at $B$ is 90° so a right angle.

Interior angles of a triangle sum to 180°.

$(AB)^2 + (BC)^2 = (AC)^2$
What is the next step for the proof that "The sum of the interior angles in any polygon is $180(n − 2)$ where $n$ is the number of sides" ?

The angles in a polygon sum to $180(n-2)$ where $n$ is the number of sides.

The number of triangles is two less than the number of sides.

The sum of the interior angles increases by 180 every time a side is added.

The sum of the interior angles of $n$ triangles is $180n$ . ✓
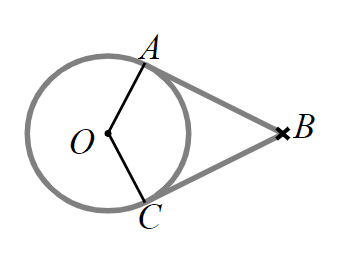Arrange the steps of this proof in order to show that "The tangents to a circle from an external point are equal in length".

1

⇔

Take a circle with centre $O$ and tangents $AB, BC$ as shown in the diagram.

2

⇔

$OA$ and $OC$ are radii so are the same length.

3

⇔

The tangents to a circle meet the radius at 90°.

4

⇔

$ABCO$ can be split into two right-angled triangles.

5

⇔

The triangles have the same hypotenuse, another side the same and a right-angle.

6

⇔

By the RHS law the triangles are congruent so length $AB=$ length $BC$ .

7

⇔

Therefore the tangents to a circle from an external point are equal in length.
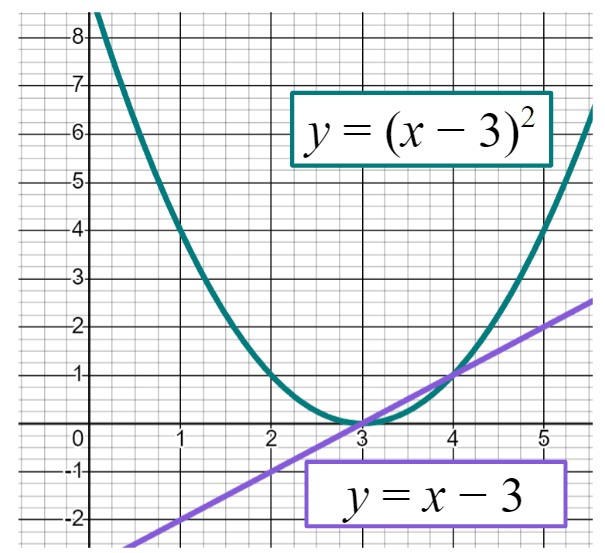Which of these values of $x$ are counterexamples to the conjecture "For all values of $x, (x-3)^2 > x-3$ "?

$x=0$

$x=2.5$

$x=3.5$ ✓

$x=4$ ✓

$x=5$
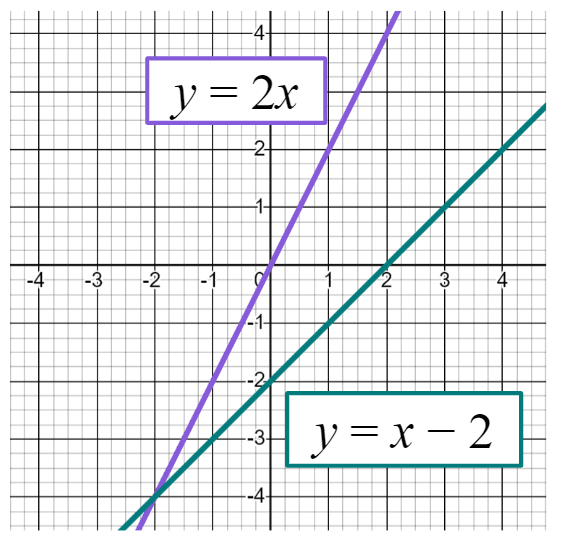Which of these best describes all the counterexamples to the conjecture "For all values of $x, 2x > x-2$ "?

The counterexamples are when $x$ is positive.

The counterexamples are when $x$ is negative.

The counterexamples are when $x \ge -2$ .

The counterexamples are when $x \le -2$ . ✓

The counterexamples are when $x \le -4$ .
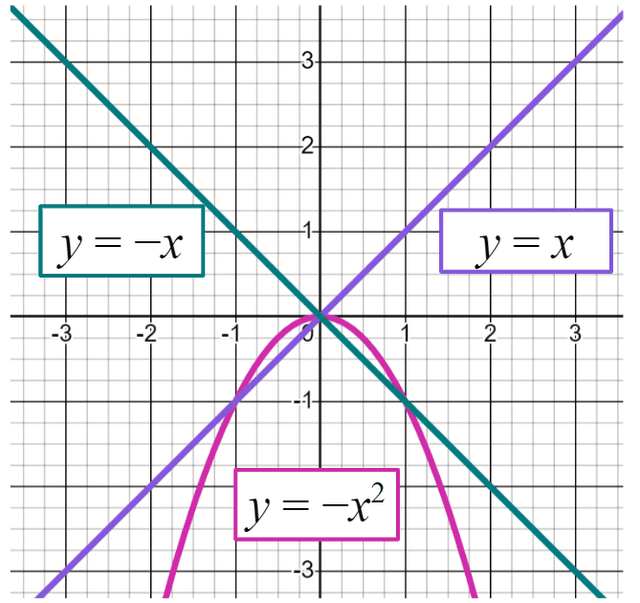Use the graphs to decide which of these conjectures are true.

For all values of $x, -x^2 \le 0$ ✓

For all values of $x, -x^2 < x$

For all values of $x, -x^2 < -x$

For all negative values of $x, -x^2 < -x$ ✓

For all integer values of $x, -x^2 < x$

Worksheet

Loading worksheet ...

Presentation

Loading presentation ...

Video

Lesson Details

Key learning points

A logical argument does not have to only be algebraic.
Geometrical reasoning can be used to argue that something is true.
Values can be used to demonstrate whether something is true.

Common misconception

Proofs have to be solely algebraic and do not involve diagrams.

Proofs involve showing that a conjecture holds for multiple cases (general case). A diagram can represent multiple cases.

Keywords

Apex - The apex is the point (vertex) which is the greatest perpendicular distance from the base.
Congruent - If one shape can fit exactly on top of another using rotation, reflection or translation, then the shapes are congruent.
Hypotenuse - The hypotenuse is the side of a right-angle triangle which is opposite the right angle.