Problem solving with further surface area and volume | Maths

Starter quiz

The amount of space occupied by a closed 3D shape is called the __________ of the shape.

area

perimeter

volume ✓
The diagram shows a composite solid constructed from two congruent cuboids. All lengths given are in centimetres. Which of these calculations give the total volume of the solid?

9 × 4 × 1 + 9 × 4 × 1

9 × 4 × 1 + 7 × 4 × 1 ✓

9 × 4 × 8

2 × (8 × 4 × 1) ✓

(1 × 8 + 8 × 1) × 4 ✓
This composite solid is constructed from two cuboids. All lengths given are in millimetres. The total volume of the solid is ______ mm³.

'238' ✓
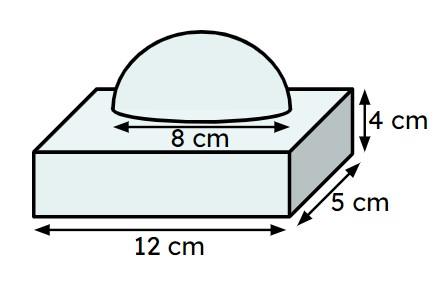This composite solid is constructed by placing a hemisphere with diameter 8 cm on top of a cuboid. Find the volume of the solid. Give your answer to the nearest cubic centimetre.

274 cm³

374 cm³ ✓

508 cm³

1312 cm³
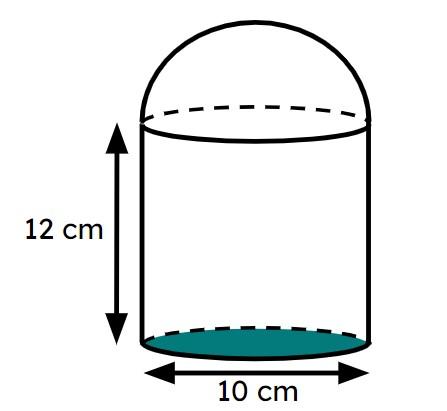This composite solid is constructed with a cylinder and a hemisphere. Each have a diameter of 10 cm. The volume of the solid is ______cm³ (correct to 4 significant figures).

'1204' ✓
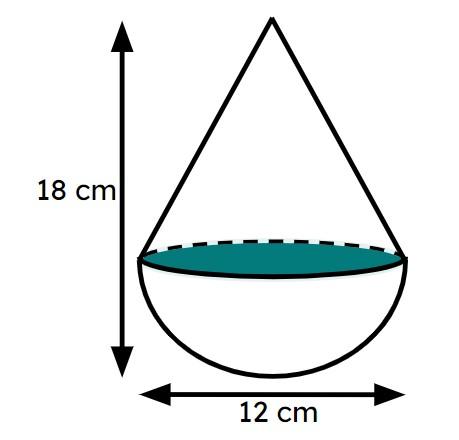This composite solid is constructed with a cone and a hemisphere. The volume of the solid, in terms of 𝜋, is ______𝜋 cm³.

'288' ✓

Exit quiz

Name a 3D shape that has exactly one curved surface and no flat surfaces.

cone

cylinder

hemisphere

prism

sphere ✓
Starting with the cuboid with the smallest volume, put these cuboids into order of size according to their volumes.

1

⇔

Red cuboid: 3 cm by 2 cm by 4 cm

2

⇔

Blue cuboid: 3 cm by 3 cm by 3 cm

3

⇔

Yellow cuboid: 2 cm by 4 cm by 6 cm

4

⇔

Green cuboid: 2 cm by 5 cm by 6 cm

5

⇔

Purple cuboid: 4 cm by 4 cm by 4 cm
Starting with the cuboid with the smallest surface area, put these cuboids into order of size according to their surface areas.

1

⇔

Red cuboid: 3 cm by 2 cm by 4 cm

2

⇔

Blue cuboid: 3 cm by 3 cm by 3 cm

3

⇔

Yellow cuboid: 2 cm by 4 cm by 6 cm

4

⇔

Purple cuboid: 4 cm by 4 cm by 4 cm

5

⇔

Green cuboid: 2 cm by 5 cm by 6 cm
In this cuboid, the depth is $k$ cm. The lengths of the depth to the height to the width of the cuboid can be written in the ratio 1 : 2 : 4. Select an expression for the volume of the cuboid.

$7k$

$7k^3$

$8k$

$8k^3$ ✓
In this cuboid, the depth is $k$ cm. The lengths of the depth to the height to the width of the cuboid can be written in the ratio 1 : 2 : 4. Find an expression for the surface area of the cuboid.

$16k^2$

$28k^2$ ✓

$14k^2$

$7k^2$
A drink can contains 33 cl of sparkling water. The can has a radius of 4 cm. The height of the can is ______ cm to 1 d.p. (assume the can is a perfect cylinder and ignore the thickness of the metal).

'6.6' ✓

Worksheet

Loading worksheet ...

Presentation

Loading presentation ...

Video

Lesson Details

Key learning points

The surface area of many solids can be calculated by a known method.
The volume of many solids can be calculated by a known method.
Writing an algebraic statement about surface area/volume can be done from a diagram.

Common misconception

Pupils may confuse whether they need to calculate the volume or surface area of a 3D shape, if not told specifically to do so in a problem.

Use the context to decide which calculation is needed. If the question refers to packaging or painting the shape, a surface area calculation is needed.

Keywords

Prism - A prism is a polyhedron with a base that is a polygon and a parallel opposite face that is identical. The corresponding edges of the two polygons are joined by parallelograms.
Cylinder - A cylinder is a 3D shape with a base that is a circle and a parallel opposite face that is identical. A cross-section of a cylinder made parallel to the base will be congruent to the base.
Surface area - The surface area is the total area of all the surfaces of a closed 3D shape. The surfaces include all faces and any curved surfaces.
Volume - Volume is the amount of space occupied by a closed 3D shape.