Using the cosine ratio | Maths | Quizalize & Oak National Academy

Starter quiz

In a right triangle, if the hypotenuse is 75 cm and a second side is 60 cm, what is the length of the third side? (Use a calculator to help you.)

50 cm

45 cm ✓

54 cm
Which of the following statements is true for these triangles?

The triangles are similar.

The triangles are not similar. ✓

It is not possible to know whether the triangles are similar or not.
In a right triangle, if the shortest sides are 7.5 cm and 18 cm, what is the length of the hypotenuse? (Use a calculator to help you.)

19.5 cm ✓

18.5 cm

20.5 cm
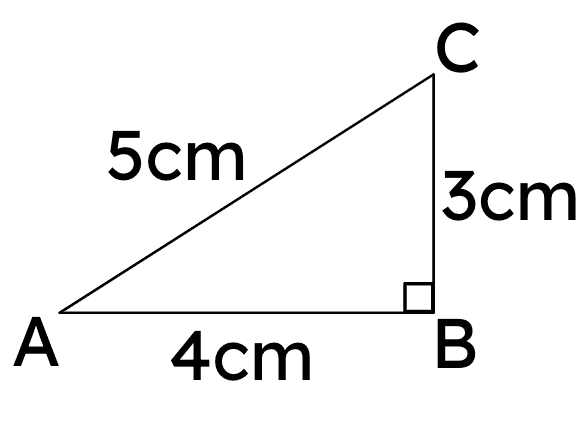Would a triangle ABC with sides AB = 16cm, BC = 10cm, AC = 21cm be similar to the one shown in the diagram?

Yes

No ✓
Would a triangle ABC with sides AB = 12 cm, BC = 9 cm, AC = 15 cm be similar to the one shown in the diagram?

Yes ✓

No
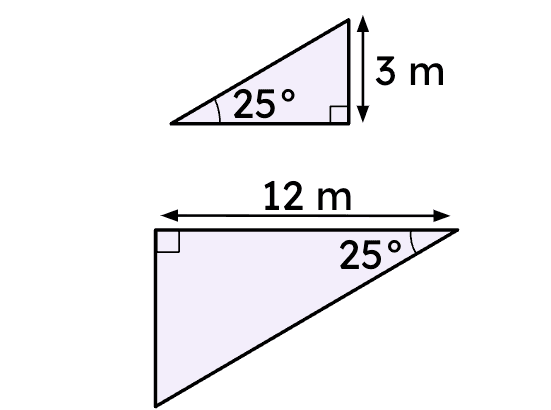For this pair of triangles, can you determine whether they are similar without using side lengths?

Yes, because their three angles correspond. ✓

No because you only know two angles.

No, because you always need a side and two angles.

Exit quiz

Using triangle ABC, if θ = 38ᵒ and hypotenuse AB = 14 cm, what is the length of the adjacent side AC to 1 d.p. ?

'11.0' ✓
What is the value of cos(20ᵒ) to 2 d.p. ?

0.93

0.94 ✓

0.92
Using triangle ABC, if θ = 38ᵒ and AC = 6 cm, what is the length of the hypotenuse AB to 1 d.p. ?

'7.6' ✓
What does the 'co' in Cosine mean?

Complementary ✓

Coordinate

Core

Conditional
Using triangle ABC, if θ = 30ᵒ and AC = 12 cm, what is the length of the hypotenuse AB to 1 d.p. ?

'13.9' ✓
Using triangle ABC, if θ = 30ᵒ and AC = 9 cm, what is the length of the hypotenuse AB to 1 d.p. ?

'10.4' ✓

Worksheet

Loading worksheet ...

Presentation

Loading presentation ...

Video

Lesson Details

Key learning points

The cosine ratio involves the hypotenuse, adjacent and the angle.
If you know the length of the hypotenuse and the size of the angle, you can use the cosine ratio.
If you know the length of the adjacent and the size of the angle, you can use the cosine ratio.
If you know the length of the hypotenuse and adjacent, you can use the cosine ratio.

Common misconception

The cosine formula is only used to find the length of a side adjacent to an angle.

The cosine formula can be used to find the length of a side adjacent to an angle. A rearrangement of the formula also allows us to find the length of the hypotenuse given the adjacent side. The arccosine function allows us to find the angle, itself.

Keywords

Hypotenuse - The hypotenuse is the side of a right-angled triangle which is opposite the right angle.
Adjacent - The adjacent side of a right-angled triangle is the side which is next to both the right angle and the marked angle.
Trigonometric functions - Trigonometric functions are commonly defined as ratios of two sides of a right-angled triangle containing the angle.
Cosine function - The cosine of an angle (cos(θ°)) is the x-coordinate of point P on the triangle formed inside the unit circle.