Scaling the right-angled triangle from the unit circle | Maths

Starter quiz

In a right triangle, if the hypotenuse is 39 cm and a second side is 15 cm, what is the area? (Use a calculator to help you.)

$270 cm^2$ ✓

$280 cm^2$

$294 cm^2$
In a right triangle, if the hypotenuse is 125 cm and a second side is 75 cm, what is the length of the third side? (Use a calculator to help you.)

$82 cm$

$100 cm$ ✓

$96 cm$
In a right triangle, if the hypotenuse is 22.5 cm and a second side is 13.5 cm, what is the perimeter? (Use a calculator to help you.)

$54 cm$ ✓

$56 cm$

$58 cm$
In a right triangle, if the shortest sides are 22.5 cm and 30 cm, what is the length of the hypotenuse? (Use a calculator to help you.)

$40.5 cm$

$37.5 cm$ ✓

$39.5 cm$
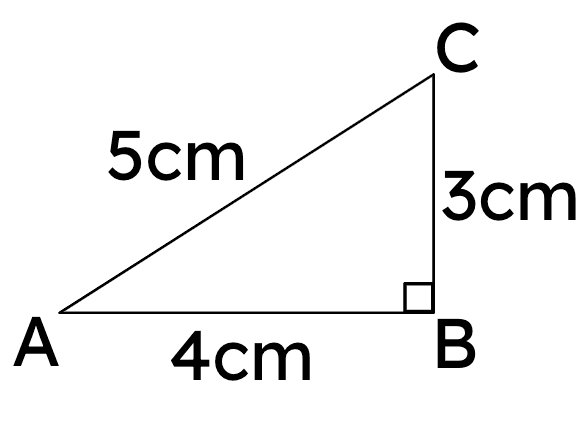Would a right triangle ABC with side AB = 24cm, and hypotenuse AC = 30cm be similar to the one shown in the diagram?

Yes ✓

No
For this pair of triangles, can you determine whether they are similar without using side lengths?

Yes, they are not similar in this case as their angles are different. ✓

No because you only know two angles.

No, because you always need a side and two angles.

Exit quiz

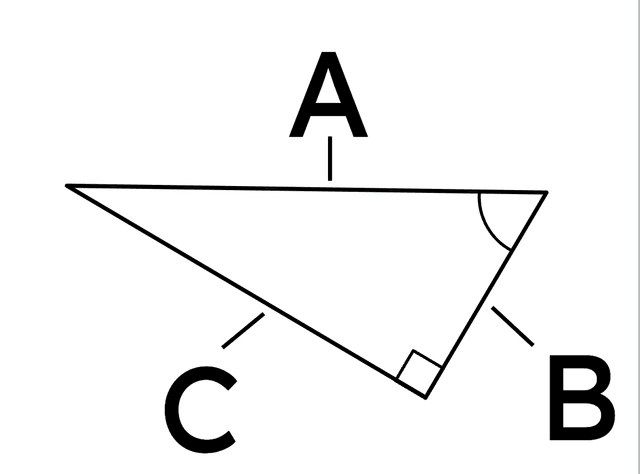Which letter represents the opposite side to the non-right angle shown in the diagram?

A

B

C ✓
Which letter represents the opposite side to the non-right angle shown in the diagram?

A ✓

B

C
Using ABCD, which side would represent the opposite if we were using angle CBD?

DC ✓

CB

BD

AD
Assuming the two triangles are similar and all measures are in cm, if length AB is 9 what is length BC?

5.4 cm ✓

7.2 cm

37 cm

6.9 cm
Assuming the two triangles are similar and all measures are in cm, if length AB is 11 what is length AC?

8.8 cm ✓

6.6 cm

11 cm

8.11 cm
Assuming the two triangles are similar and all measures are in cm, if length BC is 3.6 cm what is length AB?

4.8 cm

3.8 cm

6 cm ✓

Worksheet

Loading worksheet ...

Presentation

Loading presentation ...

Video

Lesson Details

Key learning points

There are specific ratios within the two key right-angled triangles defined by the unit circle.
The first right-angled triangle has hypotenuse of length one.
The opposite and adjacent sides of this triangle have lengths sin⁡(θ) and cos⁡(θ), respectively.
The second right-angled triangle has an adjacent side length of one.
The opposite side of this triangle has length tan⁡(θ)

Common misconception

When reading the values of the trigonometric functions during the explanation slides and the tasks, pupils may think that all the values taken from the graphs are fully accurate.

Explain that many of the values from the trigonometric functions have digits beyond the second decimal place. However, two decimal places is a reasonable degree of accuracy for reading values from the graphs during this lesson.

Keywords

Trigonometric ratios - The trigonometric ratios are ratios between each pair of lengths in a right-angled triangle.
Opposite - The opposite side of a right-angled triangle is the side which is opposite the marked angle.
Adjacent - The adjacent side of a right-angled triangle is the side which is next to both the right angle and the marked angle.