Missing angles | Maths | Quizalize & Oak National Academy

Starter quiz

In which cases are the angles always equal to each other?

adjacent angles on a straight line

alternate angles on parallel lines ✓

co-interior angles on parallel lines

corresponding angles on parallel lines ✓

vertically opposite angles ✓
Co-interior angles on parallel lines sum to ______°.

'180' ✓
Which angle is 97°?

∠BCD ✓

∠CBD

∠CDB

∠DBC
Match each shape with the sum of its interior angles.

decagon

⇔

1440° ✓

heptagon

⇔

900° ✓

hexagon

⇔

720° ✓

nonagon

⇔

1260° ✓

octagon

⇔

1080° ✓

pentagon

⇔

540° ✓
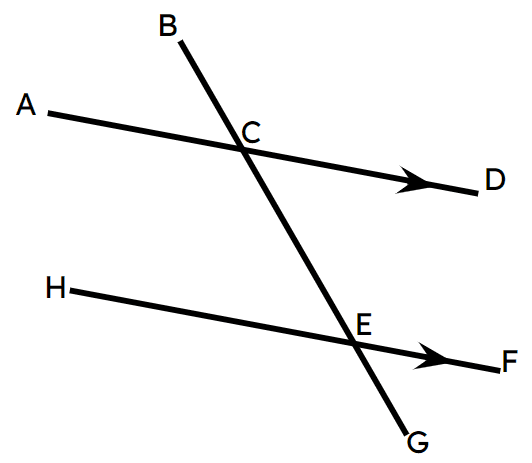∠ACE = ∠FEC because ______.

they are alternate angles on the parallel lines ✓

they are corresponding angles on the parallel lines

they are vertically opposite angles
Which angle is co-interior to ∠ACE?

∠BCA

∠CEH ✓

∠ECD

∠FEC

∠GEH

∠ABG = 112°. Based on this information, which justification could be used to explain why ∠CBG = 68°?

Adjacent angles on a straight line sum to 180°. ✓

Angles in a triangle sum to 180°.

Co-interior in parallel lines angles sum to sum to 180°.
Which justification could be used to explain why ∠CGF = ∠GCD?

Alternate angles in parallel lines are equal. ✓

Corresponding angles in parallel lines are equal.

Vertically opposite angles are equal.
Match each statement with its justification.

∠ECD = ∠CEH

⇔

alternate angles in parallel lines are equal ✓

∠DCB = ∠FEC

⇔

corresponding angles in parallel lines are equal ✓

∠ACE = ∠DCB

⇔

vertically opposite angles are equal ✓

∠BCA and ∠ACE sum to 180°

⇔

adjacent angles on a straight line sum to 180° ✓

∠ECD and ∠FEC sum to 180°

⇔

co-interior angles in parallel lines sum to sum to 180° ✓
Given ∠EGC = 82°, then ∠CGB = ______°.

'16' ✓
The pentagon in the image is regular. The size of the shaded angle is ______°.

'36' ✓
The image shows a regular pentagon and a regular hexagon. The size of the shaded angle is ______°.

'48' ✓

Loading worksheet ...

Loading presentation ...

Missing angles can be found using parallel lines.
Missing angles can be found using facts about triangles.
Missing angles can be found in polygons using knowledge of exterior and interior angles.
The relationship between interior and exterior angles can be used to find missing angles.
Missing angles can be found by using a combination of all known facts.

Pupils may work out missing angles without writing out their justifications.

Each time a number which is not on the original diagram is used or found, an explanation should be given for where it has come from.

Corresponding angles - A pair of angles at different vertices on the same side of a transversal in equivalent positions.
Alternate angles - A pair of angles both between or both outside two line segments that are on opposite sides of the transversal that cuts them.
Co-interior angles - Co-interior angles are on the same side of the transversal line and in between the two other lines.
Interior angles - An interior angle is an angle formed inside a polygon by two of its edges.
Exterior angle - An exterior angle is an angle on the outside of a polygon between an extension of an edge and its adjacent edge.