Angles on parallel lines traversed by a straight line | Maths

Starter quiz

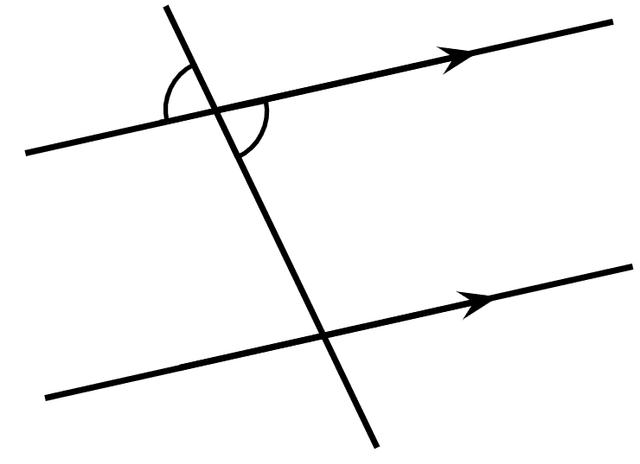
Using this diagram, you know that the angles are supplementary so $a$ is ______°.

'60' ✓
Which of these show equal angles?
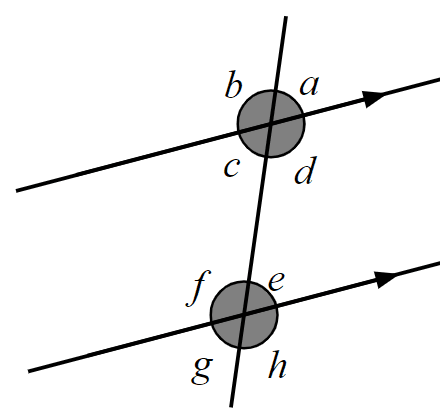Which of these pairs of angles are equal corresponding angles?

$a$ and $h$

$b$ and $f$ ✓

$c$ and $g$ ✓

$d$ and $e$

$g$ and $h$
∠______ is marked with the letter $a$ .

'PQS' ✓
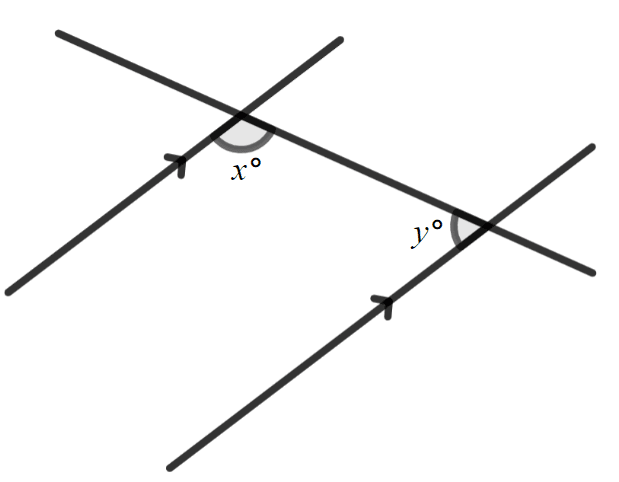Which of the following are always true statements about the angles marked $x$ and $y$ ?

$x=y+180$

$y=x+180$

$x=y$

$x+y=180$ ✓

$y=180-x$ ✓
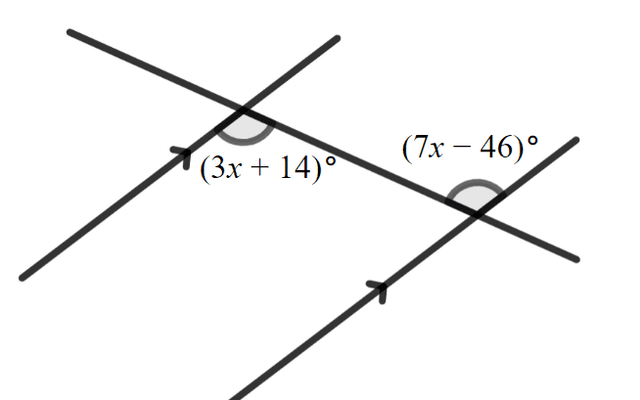$3x+14=7x-46$ as the angles are equal ______ angles.

'alternate' ✓

Two lines are parallel if they are straight lines that are always the same (non-zero) ______ apart.

'distance' ✓
For the two lines crossing the transversal to be parallel, if $c=100°$ then $g=$ ______°.

'100' ✓
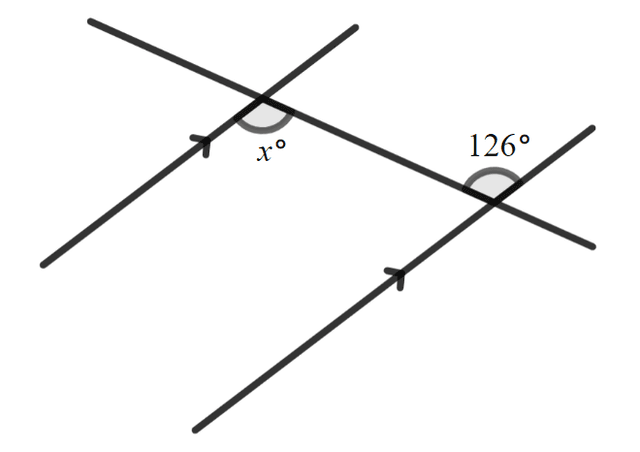Which statement about the diagram is correct?

$x° = 126°$ as the angles are equal interior alternate angles ✓

$x° = 126°$ as the angles are equal exterior alternate angles

$x° = 126°$ as the angles are equal corresponding angles
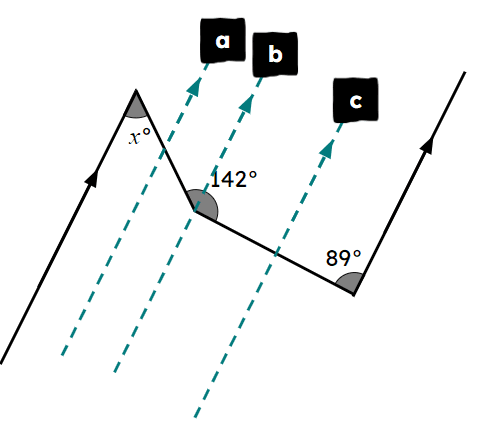Which single additional parallel line is needed on the diagram to enable you to find the value of $x$ ?

a

b ✓

c
$y°=$ ______°.

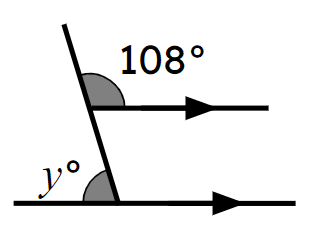'72' ✓
Which of the following statements are true?

$x=58+89$

$x=58+(180-89)$ ✓

$x=(180-58)+89$

$x=58+91$ ✓

Loading worksheet ...

Loading presentation ...

Alternate, corresponding and co-interior angles can be identified in diagrams containing pairs of parallel lines.
Facts about angles in parallel lines can be used to find unknown angles.
Facts about angles in parallel lines can be used in succession to find multiple unknown angles.

Pupils may struggle with the justifications rather than getting to the answer.

Keep asking pupils "why?" and encourage them to ask themselves, whenever they are working out an angle.

Parallel - Two lines are parallel if they are straight lines that are always the same (non-zero) distance apart.
Alternate angles - a pair of angles both between or both outside two line segments that are on opposite sides of the transversal that cuts them.
Corresponding angles - Corresponding angles are a pair of angles at different vertices on the same side of a transversal in equivalent positions.
Co-interior angles - o-interior angles are on the same side of the transversal line and in between the two other lines.
Vertically opposite angles - Vertical angles are pairs of opposite angles formed when two lines intersect at a point. They are equal.