Alternate angles | Maths | Quizalize & Oak National Academy

Starter quiz

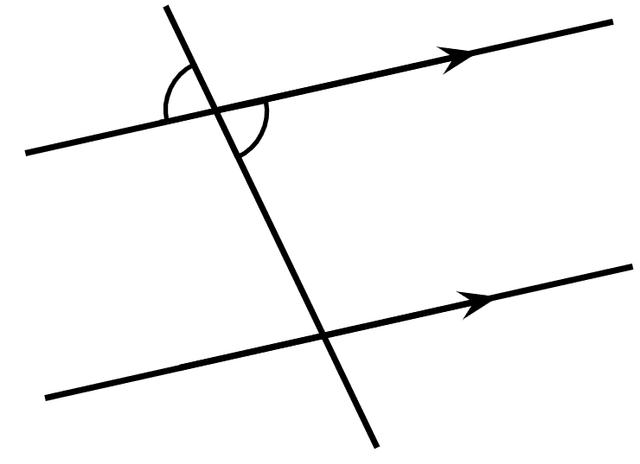
The size of the angle marked $a$ is ______°.

'56' ✓
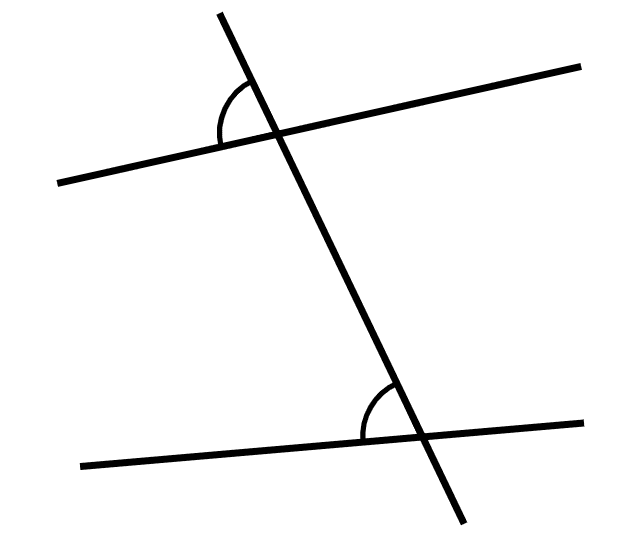
The value of the angle marked $x$ is ______°.

'88' ✓
Work out the value of $m$ .

20

107 ✓

127

160
Which pair of line segments are parallel to each other in this diagram?

AE

BF ✓

IJ

CG ✓

AB
A transversal is any line that ______ two or more lines at distinct (different) points.

'intersects' ✓
Which of the following show a pair of corresponding angles?

Alternate angles are a pair of angles both between or both outside two line segments that are on ______ sides of the transversal that cuts them.

'opposite' ✓
Which of these diagrams show a pair of alternate angles?
This diagram shows a pair of equal ______ alternate angles.

'exterior' ✓
Select the correct justification for the statement. The angle marked $m$ is 118°.

Because it is an interior alternate angle with the given angle.

Because it is an exterior alternate angle with the given angle.

Because it is an equal interior alternate angle with the given angle. ✓

Because it is an equal exterior alternate angle with the given angle.
If alternate angles are equal, then the two lines are __________.

parallel ✓

perpendicular

the same length

different
Use this diagram to match each angle to an equal alternate angle.

a

⇔

g ✓

b

⇔

h ✓

c

⇔

e ✓

d

⇔

f ✓

Loading worksheet ...

Loading presentation ...

Alternate angles can be identified in an arrangement of 3 line segments.
If two of the lines are parallel these alternate angles are equal.
Knowledge of alternate angles can be used to find unknown angles.
Knowledge of corresponding and alternate angles can be used to find unknown angles.

Referring to alternate angles as 'Z' angles because of the arrangement of the lines.

Modelling the justification correctly through every example and using exterior alternate angles to highlight the limitations of 'Z' angles.

Alternate angles - A pair of angles both between or both outside two line segments that are on opposite sides of the transversal that cuts them.